La antaŭa programo havas kiel ĉefan avantaĝon ekspluati la nature rekursivan strukturon de la fraktala solido.
Rimarku ke tiu sama metodo povas esti uzata ankaŭ por generi aliajn fraktalajn solidojn aŭ, pli simple, aliajn
fraktalajn kurbojn. Ĉiuokaze, la tuja konsekvenco de la rekursiva pritrakto estas mallonga fontokodo kaj simple
komprenebla. Bedaŭrinde, rimarku ke spongo je 3-a ordo postulas jam 48000 kvadratojn. Necesas tiam estigi la
memoron dediĉitan al XLogo je 256 MB en la fenestro pri preferoj por ke la programo povu ruliĝi
tute.
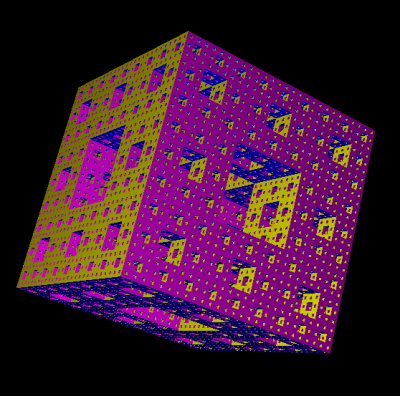
Se oni deziras grafiki Menger-an spongon je 4-a ordo, baldaŭ oni estos barita de forĉerpado de memoro. En ĉi tiu
parto ni vidos programon bazitan sur tute malsama algoritmo; ĝi ebligos krei spongon de Menger je ordo 0, 1, 2, 3
aŭ 4.
La spongo de Menger estas efektive ĝeneraligon en 3 dimensioj de ebena figuno nomata tapiŝo de Sierpinski. Jen la
unuaj iteracioj de tiu figuro:

Stadio 0

Stadio 1

Stadio 2

Stadio 3
La motivo estanta sur ĉiu faco de spongo de Menger je ordo p-a estas tapiŝo de Sierpinski je ordo
p-a.
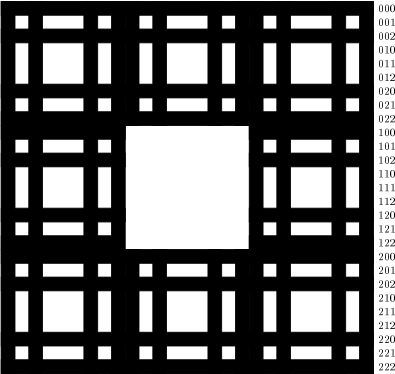
La celo estas atingi malpligrandigi la nombron de postulitaj kvarlateroj por desegni tapiŝon de Sierpinski. La jena
ekzemplo klarigas la la procedon uzitan por krei tapiŝon de Sierpinski je ordo 3-a. Ĉi tie, la komenca kvadrato
konsistas do el 33 = 27 horizontaloj kaj 27 vertikaloj. Oni skribas je bazo 3 la numeron de ĉiu horizontalo kaj ĉiu
vertikalo.
- Unua stadio: Por ĉiu horizontalo kies numero konsistas el neniu 1, grafiku horizontalon de 27 ĉeloj. Pro
simetrio, efektivigu la saman operacion vertikale.
- Dua stadio: Nun interesiĝu pri la horizontaloj kies numero konsistas el ununura 1 en l’ unua loko. Grafiku
sinsekve alterne ortangulojn longaj je 9 ĉeloj. Faru por la vertikaloj simetrie.
- Tria stadio: Nun interesiĝu pri la horizontaloj kies numero konsistas el nur unu 1 en la dua loko. Grafiku
sinsekve alterne ortangulojn laŭ la skemo [3 3 6 3 6 3 3] (3 ĉeloj plenaj, 3 malplenaj, 6 plenaj, ktp...).
Simetrie faru por la vertikaloj.
- Lasta stadio: Interesiĝu pri horizontaloj kies numero konsistas el du 1 lokitaj en l’ unuaj lokoj. Grafiku
sinsekve alterne ortangulojn laŭ la skemo [3 3 3 9 3 3 3]. Operaciu same por la vertikaloj.
Tiam finiĝas la konstruado de la tapiŝo de Sierpinski je ordo 3-a. Por krei tiun tapiŝon necesis uzi entute:
16 + 16 + 32 + 16 = 80 ortangulojn.
Por resumi la antaŭan konstruadon, jen la malsamaj tipoj de skemaj de vertikaloj laŭ ilia numero. (La simbolo *
indikas la ciferon 0 aŭ la ciferon 2.
|
|
| Numero de la tipo | Skemo aplikenda |
|
|
| *** | 27 |
|
|
| 1** | 9 9 9 |
|
|
| *1* | 3 3 6 3 6 3 3 |
|
|
| 11* | 3 3 3 9 3 3 3 |
|
|
| |
Sur la sama principo, por krei tapiŝon je ordo 4-a, oni uzu kvadraton kun 34 = 81 ĉeloj. La numeroj de
horizontaloj kaj vertikaloj havos do 4 ciferojn en ilia prezentado je bazo 3. Por ĉiu tipo de numero, jen la skemo
aplikenda (la simbolo * indikas la ciferon 0 aŭ la ciferon 2):
|
|
| Numero de tipo | Skemo aplikenda |
|
|
| **** | 81 |
|
|
| 1*** | 27 27 27 |
|
|
| *1** | 9 9 18 9 18 9 9 |
|
|
| **1* | 3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3 |
|
|
| *11* | 3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3 |
|
|
| 1*1* | 3 3 6 3 6 3 3 27 3 3 6 3 6 3 3 |
|
|
| 11** | 9 9 9 27 9 9 9 |
|
|
| 111* | 3 3 3 9 3 3 3 27 3 3 3 9 3 3 3 |
|
|
| |
496 kvarlateroj estas do necesaj por grafiki tapiŝon de Sierpinski je ordo
4.
Finfine, jen la konstruskemoj por solidoj je ordo 2:
|
|
| Numero de tipo | Skem’ aplikenda |
|
|
| ** | 9 |
|
|
| 1* | 3 3 3 |
|
|
| |
# Grafikas tapi^son de Sierpinski je ordo :p kaj je amplekso :amplekso
por tapiŝo :amplekso :p
provizu "unuo :amplekso / (potencon 3 :p)
se :p=0 [ort :amplekso :amplekso haltu]
se :p=1 [ripetu 4 [ort :amplekso :unuo an :amplekso dn 90] haltu]
ripetupor (list "x 1 potencon 3 :p)
[lokp "cantorx cantor :x :p []
# Ne grafiku la erojn havantajn unu 1 en la lasta loko
se ne (1 = lastan :cantorx)
[lokp "nom valorigu senlastan :cantorx "
grafiku_vertikalon :x econ_sendu "map :nom]]
fino
# Donas la nombron x je bazo 3
# p profundeca indekso 3^p
# :list listo malplena ĉe l’ komenco
por cantor :x :p :list
se :p=0 [sendu :list]
lokp "a potencon 3 :p-1
se :x <= :a
[sendu cantor :x :p-1 frazon :list 0]
[se :x <= 2*:a [sendu cantor :x-:a :p-1 frazon :list 1]
sendu cantor :x - 2*:a :p-1 frazon :list 0]
fino
# Grafiku la x-an vertikalon laŭ la konstruskemo difinita en la listo
por grafiku_vertikalon :x :list
l dn 90 an (:x-1)*:unuo mdn 90 ml des :list
l mdn 90 an (:x-1)*:unuo mdn 90 an :x*:unuo dn 90 ml des :list
l mdn 90 man :x*:unuo ml
fino
# Grafiku ortangulon laŭ donitaj dimensioj
# Ĝin registras la 3d-vidilo
por ort :lo :la
provizu "nombrilo :nombrilo + 1
por_edro
ripetu 2 [an :lo dn 90 an :la dn 90]
fino_edro
fino
# Pretigu la malsamajn eblajn vertikalojn por la tapiŝoj je ordo 1 al 4
por pretmap
econ_provizu "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
econ_provizu "map 110 [9 9 9 27 9 9 9]
econ_provizu "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
econ_provizu "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
econ_provizu "map 000 [81]
econ_provizu "map 100 [27 27 27]
econ_provizu "map 010 [9 9 18 9 18 9 9]
econ_provizu "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
econ_provizu "map 01 [3 3 6 3 6 3 3]
econ_provizu "map 00 [27]
econ_provizu "map 10 [9 9 9]
econ_provizu "map 11 [3 3 3 9 3 3 3]
econ_provizu "map 1 [3 3 3]
econ_provizu "map 0 [9]
fino
# Se la prezento estas [1 0 1] --> sendu 101
por valorigu :list :vort
se malplena? :list [sendu :vort]
[lokp "vort vort :vort unuan :list
sendu valorigu senunuan :list :vort]
fino
# Desegnu la ortangulojn de ĉiu vertikalo alterne
por des :list
lokp "sumo 0
ripetupor (list "i 1 kmpt :list)
[lokp "ero eron :i :list
lokp "sumo :ero + :sumo
se para? :i [l an :ero*:unuo ml] [ort :ero*:unuo :unuo an :ero*:unuo]]
l man :sumo * :unuo ml
fino
# Testu ĉu nombro estas para
por para? :i
sendu 0 = reston :i 2
fino
por siertapiŝo :p
ev perspektive tdk pretmap
provizu "nombrilo 0
tapiŝo 810 :p
tajpu "Nombro\ de\ kvarlateroj:\ s :nombrilo
vue3d
fin
siertapiŝo 3 desegnas tapiŝon de Sierpinski je ordo 3 kaj latero 810. Jen, ni pretas pasi al la spongo de
Menger!
La spongo de Menger havas plurajn simetriecajn atributojn. Por generi ĝin ni grafikos la diversajn sekciojn laŭ la
ebeno (xOy), poste portos tiujn figurojn laŭ (yOz) kaj (xOz). Por bone klarigi tion kio okazas, ni restu sur l’
ekzemplo de la spongo je ordo 3:
Kiam oni tranĉas la spongon laŭ vertikala ebeno, oni povas akiri kvar malsamajn motivojn:
Por grafiki spongon je ordo 3, ni trairos la nombrojn de 1 ĝis 27, tio estas, de 001 ĝis 222 je bazo 3. Por ĉiu
numero, oni aplikos la taŭgan sekcion kiun oni portos laŭ la 3 direktoj (Ox), (Oy) kaj (Oz).
La jena programo permesas grafiki la solidojn de Menger je ordoj 0, 1, 2, 3, 4. La nombro de proceduroj estas grava,
do mi klarigos tuj.
# Grafiki tapiŝon de Sierpinski je ordo :p kaj je amplekso :amplekso
por tapiŝo :amplekso :p
provizu "unuo :amplekso / (potencon 3 :p)
se :p=0 [ort :amplekso :amplekso haltu]
se :p=1 [ripetu 4 [ort :amplekso :unuo an :amplekso dn 90] haltu]
ripetupor (list "x 1 potencon 3 :p)
[lokp "cantorx cantor :x :p []
# Ne grafiku erojn havantajn unu 1 en la lasta loko
se ne (1 = lastan :cantorx)
[lokp "nom valorigu senlastan :cantorx "
grafikuvertikalon :x econ_sendu "map :nom]]
fino
# Sendu la prezenton je bazo 3 de la nombro x
# p profundeca indekso 3^p
# :list listo malplena ĉe l’ komenco
por cantor :x :p :list
se :p=0 [sendu :list]
lokp "a potencon 3 :p-1
se :x <= :a
[sendu cantor :x :p-1 frazon :list 0]
[se :x <= 2*:a [sendu cantor :x-:a :p-1 frazon :list 1]
sendu cantor :x-2*:a :p-1 frazon :list 2]
fino
# Grafiku la numeron x laŭ la konstruskemo difinita en la listo
por grafikuvertikalon :x :list
l dn 90 an (:x-1)*:unuo mdn 90 ml des :list
l mdn 90 an (:x-1)*:unuo dn 90 an :x*:unuo dn 90 ml des :list
l mdn 90 man :x*:unuo ml
fino
# Grafiku ortangulon laŭ donitaj dimensiojn
# La plurlatero estas registrita de la 3d-vidigilo
por ort :lo :la
provizu "nombrilo :nombrilo+1
por_edro
ripetu 2 [an :lo dn 90 an :la dn 90]
fino_edro
fino
# Komencu la malsamajn vertikalojn eblajn por la tapiŝojn je ordo 1 ĝis 4
por pretmap
econ_sendu "map 111 [3 3 3 9 3 3 3 27 3 3 3 9 3 3 3]
econ_sendu "map 110 [9 9 9 27 9 9 9]
econ_sendu "map 101 [3 3 6 3 6 3 3 27 3 3 6 3 6 3 3]
econ_sendu "map 011 [3 3 3 9 3 3 6 3 3 9 3 3 6 3 3 9 3 3 3]
econ_sendu "map 000 [81]
econ_sendu "map 100 [27 27 27]
econ_sendu "map 010 [9 9 18 9 18 9 9]
econ_sendu "map 001 [3 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 6 3 3]
econ_sendu "map 01 [3 3 6 3 6 3 3]
econ_sendu "map 00 [27]
econ_sendu "map 10 [9 9 9]
econ_sendu "map 11 [3 3 3 9 3 3 3]
econ_sendu "map 1 [3 3 3]
econ_sendu "map 0 [9]
fino
# Se la prezento estas [1 0 1] --> sendu 101
# Se la prezento estas [1 0 2] --> sendu 100
# La eroj de la listo estas kunmetataj en vorton.
# Krome, la 2 estas anstataŭataj de nuloj
por valorigu :list :vort
se malplena? :list [sendu :vort]
[lokp "unua unuan :list
se :unua=2 [lokp "unua 0]
lokp "vort vort :vort :unua
sendu valorigu senunuan :list :vort]
fino
# Desegnu la ortangulojn de ĉiu vertikalo alterne
por des :list
lokp "sumo 0
ripetupor (liston "i 1 kmpt :list)
[lokp "ero eron :i :list
lokp "sumo :ero+:sumo
se para? :i [l an :ero*:unuo ml] [ort :ort*:unuo :unuo an :ero*:unuo]]
l man :sumo * :unuo ml
fino
# Testu ĉu nombro estas para
por para? :i
sendu 0 = resto :i 2
fino
por siertapiŝo :p
ev perspektive tdk pretmap
provizu "nombrilo 0
tapiŝo 810 :p
tajpu "Nombro\ de\ plurlateroj:\ s :nombrilo
tridimensie_vidigu
fino
# Forigas la lastan 1 en la listo :list
por forigulastanunu :list
ripetupor (list "i kmpt :list 1 minusigan 1)
[lokp "ero eron :i :list
se :ero=1 [lokp "list anstataŭigu :list :i 0 haltu] [se :ero=2 [haltu]]]
sendu :list
fino
# Spongo de Menger je amplekso donita kaj je profundeco :p
por menger :amplekso :p
provizu "unuo :amplekso / (potencon 3 :p)
ripetupor (list "z 1 potencon 3 :p)
[lokp "cantorz cantor :z :p []
lokp "last lastan :cantorz
lokp "cantorz senlantan :cantorz
se :last=0 [lokp "ordo valorigu forigulastanunu :cantorz "] [lokp "ordo valorigu :cantorz "]
lokp "ordo vort "tranĉi :ordo
graf3tapiŝon :amplekso :ordo :z
l supren 90 an :unuo malsupren 90 ml]
graf3tapiŝon :amplekso :ordo (potencon 3 :p) + 1
fino
# Grafiku la tapiŝojn de Sierpinski je ordo :p
# laŭ ĉiu akso (Ox), (Oy) et (Oz)
# je la alto :z
pour draw3carpet :size :order :z
l originen
supren 90 an (:z-1)*:unuo malsupren 90 ml
skolp bluan ekzek :ordo :amplekso
l originen
mdfn 90 an (:z-1)*:unuo malsupren 90 ml
skolp flavan ekzek :ordo :amplekso
l originen
supren 90 an :amplekso dn 90 an (:z-1)*:unuo malsupren 90 ml
skolp violruĝan ekzek :ordo :amplekso
fino
# Ĉefa proceduro
# Grafiku spongon de Menger je profundeco :p
por spongo :p
ev perspektive tdk
lokp "tempo tempon
pretmap
provizu "nombrilo 0
se :p=0 [kubo 405] [menger 405 :p]
# Skribu la tempon kaj la nombron de plurlateroj necesaj por konstrui
tajpu "Nombro\ de\ plurlateroj:\ s :nombrilo
tajpu "Tempo\ uzita:\ s tempon - :tempo
tridimensie_vidigu
fino
# Sekcio por la Menger je ordo 2
por tranĉi1 :amplekso
ripetu 4 [tapiŝu :amplekso/3 1 l an :amplekso dn 90 ml]
fino
por tranĉi0 :amplekso
tapiŝo :amplekso 2
fino
# Sekcio por la Menger je ordo 3
por tranĉi10 :amplekso
ripetu 4 [tapiŝo :amplekso/3 2 l an :amplekso dn 90 ml]
fino
por tranĉi01 :amplekso
ripetu 4 [ripetu 2 [tranĉi1 :amplekso/3 l an :amplekso/3 ml] an :amplekso/3 dn 90]
fino
por tranĉi11 :amplekso
ripetu 4 [tranĉi1 :amplekso/3 l an :amplekso dn 90 ml]
fino
por tranĉi00 :amplekso
tapiŝo :amplekso 3
fino
# Sekcio por la Menger je ordo 4
por tranĉi000 :amplekso
tapiŝo :amplekso 4
fino
por tranĉi100 :amplekso
ripetu 4 [tapiŝo :amplekso/3 3 l an :amplekso dn 90 ml]
fino
por tranĉi010 :amplekso
ripetu 4 [ripetu 2 [tranĉi10 :amplekso/3 l an :amplekso/3 ml] an :amplekso/3 dn 90]
fino
por tranĉi001 :amplekso
ripetu 4 [ripetu 2 [tranĉi01 :amplekso/3 l an :amplekso/3 ml] an :amplekso/3 dn 90]
fino
por tranĉi110 :amplekso
ripetu 4 [tranĉi10 :amplekso/3 l an :amplekso ml dn 90]
fino
por tranĉi111 :amplekso
ripetu 4 [tranĉi11 :amplekso/3 l an :amplekso dn 90 ml]
fino
por tranĉi101 :amplekso
ripetu 4 [tranĉi01 :amplekso/3 l an :amplekso dn 90 ml]
fino
por tranĉi011 :amplekso
ripetu 4 [ripetu 2 [tranĉi11 :amplekso/3 l an :amplekso/3 ml] an :amplekso/3 dn 90]
fino
por tranĉi :amplekso
tapiŝo :amplekso 1
fino
por kubo :amplekso
ripetu 2
[skolp bluan ort :amplekso :amplekso l an :amplekso malsupren 90 ml
skolp flavan ort :amplekso :amplekso l an :amplekso malsupren 90 ml]
skolp violruĝan
l mdfn 90 mdn 90 an :amplekso dn 90 ml ort :amplekso :amplekso
l dn 90 an :amplekso mdn 90 dfn 90 dn 90 an :amplekso mdn 90 dfn 90 ml ort :amplekso :amplekso
mdfn 90 mdn 90 an :amplekso dn 90
fino
por kuboj
ev perspektive tdk
lokp "tempo tempon
pretmap
provizu "nombrilo 0
ripetu 4 [se komputu = 1 [kubo 405] [menger 405 komputu-1] l an 1000 dn 90 ml]
# Montru la tempon uzitan kaj la nombron de plurlateroj necesaj por konstrui
tajpu "Nombro\ de\ plurlateroj:\ s :nombrilo
tajpu "Tempo\ uzita:\ s tempon - :tempo
tridimensie_vidigu
fino
Nun, establu la memoron rezervitan por XLOGO je 640 MiB: spongo 4